Consider resistor shown in the Fig. 1. The resistance R1, R2 and R3
are said to be in series. The combination is connected across a source
of a voltage V volts. Naturally the current flowing through all of them
is same indicated as I amperes. e.g. the small chain of small lights,
used for the decoration purposes is good example of series combination.
Now let us study the voltage distribution
 |
| Fig. 1 A series circuit |
Let V1, V2 and V3 be the voltages across the terminals of resistances R1, R2 and R3 respectively,
Then V = V1 +V2 + V3
Now according to Ohm's law V1 = I R1 , V2 = I R2 , V3 = I R3
Current through of them is same i.e. I
V = I R1 + I R2 + I R3 = I (R1 +R2 +R3 )
Applying Ohm's law to overall circuit
Now according to Ohm's law V1 = I R1 , V2 = I R2 , V3 = I R3
Current through of them is same i.e. I
V = I R1 + I R2 + I R3 = I (R1 +R2 +R3 )
Applying Ohm's law to overall circuit
V = I Req
Where Req = Equivalent resistance of the circuit, by comparison of tow equations,
Req = R1 + R2 + R3
i.e. total or equivalent resistance of the series circuit is arithmetic sum of the resistances connected in series
For n resistances in series, R = R1 + R2 + R3 +.......+ Rn
Characteristic of series circuits
1) The same current flows through each resistance.
2) The supply voltage V is the sum of the individual voltage drops across the resistances.
V = V1 +V2 + ..... + Vn
3) The equivalent resistance is equal to the sum of the individual resistances
4) The equivalent resistance is the largest of all the individual resistances.
i.e R >R1 , R >R2 , ..........R > Rn
2. Inductors in series
Consider in the Fig. 2(a). Tow inductors L1 and L2 are connected in series. The current flowing through L1 and L2 are i1 and i2 while voltages developed across L1 and L2 are VL1 and VL2 respectively. The equivalent circuit as shown in the Fig. 2(b).
 |
| Fig. 2 |
For series combination,
i = i1 = i2
and VL = VL1 + VL2
... Leq di/dt = L1 di/dt + L2 di/dt
... Leq di/dt = (L1 +L2 ) di/dt
... Leq = L1 +L2
That means, equivalent inductances of the series combination of tow
inductances is the sum of inductances connected in series
The total equivalent inductances of the series circuit is the sum of the inductances connected in series.
For n inducatances in series,
Leq = L1 + L2 + L3 + ............+ Ln
3. Capacitors in series
Consider the Fig. 3(a). Tow capacitors C1 and C2 are connected in series. The current flowing through and voltages developed across C1 and C2 are i1, i2 and VC1 and VC2 respectively. The equivalent circuit is shown in the Fig. 3(b).
 |
| Fig. 3 |
For series combination,
i = i1 = i2 and
VC = VC1 + VC2
But i = i1 = i2
That means,
reciprocal of equivalent capacitor of the series combination is the sum
of the reciprocal of individual capacitances.
The reciprocal of the total equivalent capacitors of the series
combination is the sum of the reciprocols of the individual capacitors,
connected in series,


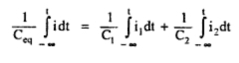
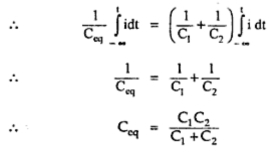






No comments:
Post a Comment