1.1 Power Factors Referred to Receiving End Voltage
Consider an A.C. distribution PQ having concentrated loads of I1 and I2 tapped off at point Q and R respectively. This is shown in the Fig. 1.
 |
| Fig. 1 |
Let voltage VQ which is the voltage at the receiving end be taken as reference vector. The power factors at R and Q are cosΦ1 and cosΦ2 with respect to VQ and they are lagging.
Let, R1 = Resistance of section PR
X1 = Reactance of section PR
R2 = Resistance of section RQ
X2 = Reactance of section RQ
As shown in the Fig. 2. the receiving end voltage VQ is taken as reference vector. The currents I1 and I2 are lagging from VQ by angles of Φ1 and Φ2 respectively. The vector sum of I1 and I2 gives current IPR. The drop is I2R2 in phase with I2 while I2X2 is leading by 90o. The vector sum of VQ, I2R2 and I2X2 gives VR. The drop IPRR1 is in phase with current IPR while IPRX1 is leading by 90. The vector sum of VR, IPRR1 and IPRX1 gives the sending end voltage.
1.2 Power Factors Referred to Respective Load Voltages
In previous section we have considered the load power factors with
respect to receiving end voltage. Here we will consider these power
factors with respect to their respective load voltages. Now Φ1 is the phase angle between VR and I1 while the angle Φ2 is the phase angle between VQ and I2.
Here again the receiving end voltage VQ is the reference phasor. The vector sum of I1 and I2 gives the current IPR. The drop I2R2 is in phase with I2 while I2X2 is leading by 90. The vector sum of VQ, I2R2 and I2X2 gives voltage VR. The drop IPRR1 is in phase with current IPR while the drop IPRX1 is leading by 90o. The vector sum of VR, IPRR1 and IPRX1 gives the sending end voltage Vp.









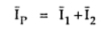









No comments:
Post a Comment